9 ශ්‍රේණිය විද්‍යාව : බලය පිලිබඳ සංකල්ප - 2

පසුගිය ලිපියෙන් බලය හා බලයේ විශාලත්වය පිළිබඳව අධ්‍යනය කෙරුණු අතර මෙම ලිපියෙන් බලයේ දිශාව හා බලයේ රුපික නිරුපණය පිළිබඳව සලකා බලමු.

 

ක්‍රිකට් ක්‍රීඩාවේදී පිතිකරුවෙකු පිත්ත හසුරුවන දිශාව අනුව බෝලයේ ගමන් මාර්ගය වෙනස් වේ. එනම් බෝලය මත බලය යෙදෙන දිශාව අනුව බෝලය ගමන් කරන දිශාවද වෙනස් වේ. තවද දොරක් වැසීමට අපි එම දොර තල්ලු කරන්නේ නම් එය ඇරීමට ඇදිය යුතු වේ. ඒ අනුව බලයේ දිශාව අනුව අපට ලැබෙන ප්‍රතිඵල එකිනෙකට වෙනස් වේ.  

 

දැන් අපි මේසය මත තබා ඇති මල් බඳුනක් සලකමු. එහි පතුලට ආසන්නයෙන් බලයක් ලබා දීමෙන් ඔබට එය මේසය දිගේ තල්ලු කල් හැකි වුවත් එහි ඉහල කෙලවරට ආසන්නයෙන් බලයක් ලබා දීමෙන් එය මේසය මතට පෙරළේ. ඒ අනුව බලය යොදන ලක්ෂ්‍යය අනුවද අපට ලැබෙන ප්‍රතිඵල එකිනෙකට වෙනස් වේ. මෙසේ වස්තුවක් චලනය කිරීම සඳහා බලයක් යොදන ලක්ෂ්‍යය එම බලයේ උපයෝගී ලක්ෂ්‍යය නමින් හැඳින්වේ.

 

ඒ අනුව බලයක් පිළිබඳව අධ්‍යනය කිරීමේදී බලයේ විශාලත්වය, බලය ක්‍රියා කරන දිශාව මෙන්ම බලයේ උපයෝගී ලක්ෂ්‍යය පිළිබඳවද සැලකිලිමත් විය යුතු වේ. විශාලත්වයක් මෙන්ම දිශාවක්ද ඇති රාශීන් දෛශික රාශි ලෙස හැඳින්වෙන බැවින් බලයද දෛශික රාශියක් වේ.

 

බලයක් රුප සටහනක් ආධාරයෙන් නිරුපණය කරන ආකාරය මීළඟට සලකා බලමු. එහිදී සරල රේඛා ඛණ්ඩයක් යොදා ගෙන බලයේ විශාලත්වය එම සරල රේඛා ඛණ්ඩයේ දිගින්ද, බලයේ දිශාව සරල රේඛා ඛණ්ඩය මත ඇඳි ඊ හිසෙන්ද, බලයේ උපයෝගී ලක්ෂ්‍යය එම සරල රේඛා ඛණ්ඩය මත ඇඳි තිතකින්ද නිරුපණය කෙරේ.

උදාහරණක් ලෙස පෙට්ටියක් මත තිරස්ව දකුණු දිශාවට යෙදෙන 3N බලයක්ද ඒ මත සිරස්ව ඉහලට යෙදෙන 6N බලයක්ද සලකමු. එහිදී බල රුප සටහන පහත පරිදි විය යුතුය.

 

 

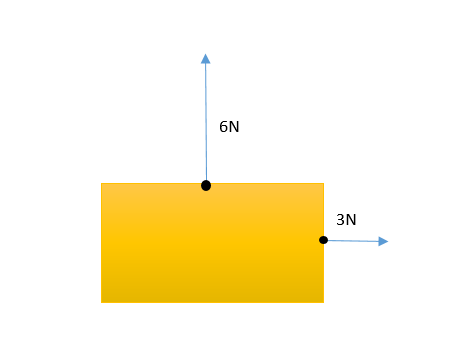
මෙහිදී බලවල විශාලත්ව සැලකීමේදී  6N බලය නිරුපණය කරන සරල රේඛා ඛණ්ඩයේ දිග 3N බලය නිරුපණය කරන සරල රේඛා ඛණ්ඩයේ දිග මෙන් දෙගුණයක් විය යුතුය.

 

අපි එදිනෙදා ජීවිතයේ සෑම කාර්යයකදීම පාහේ බල යොදා ගන්නා අතර ඒ සඳහා අපට යම් කිසි වෙහෙසක්ද දැරීමට සිදු වේ. මෙම වෙහෙස අවම කර ගැනීම සඳහා මිනිසා බලය යොදන දිශාව මෙන්ම බලයේ උපයෝගී ලක්ෂ්‍යයද සුදුසු පරිදි වෙනස් කර ගැනීමට පෙළඹේ.

 

 

 

 

 

 

 

මෙම රුපයේ දැක්වෙන්නේ එවැනි අවස්ථාවන්ට උදාහරණ වේ. පළමු රුපයේ මිනිසා කරත්තය තල්ලු කිරීමේ පහසුව සඳහා ඊට මිටක් සවි කර ඔහුගේ දෑත්  මට්ටමට බලයේ උපයෝගී ලක්ෂ්‍යය රැගෙන ඇත. දෙවෙන රුපයේ මිනිසා පෙට්ටිය ඇදීමේ පහසුව සඳහා තිරස්ව බලය යෙදිම වෙනුවට  ඔහුට පහසු දිශාව ඔස්සේ බලය යොදන දිශාව වෙනස් කරගෙන ඇත. ඒ අනුව බල පිළිබඳව හොඳින් අධ්‍යනය කිරීමෙන් අවම වෙහෙසකින් වැඩි කාර්ය ප්‍රමාණයක් නිම කිරීමට හැකියාව ලැබෙනු ඇත.

 

 

 

 

 

 

 

 

 

by D.S.Ishanthi.

Photo source : Internet